初探二叉树的应用

树的性质

二叉树的性质

关于树和二叉树的更多性质和应用见：树的概念和应用_摘自2015年数据结构联考复习指导

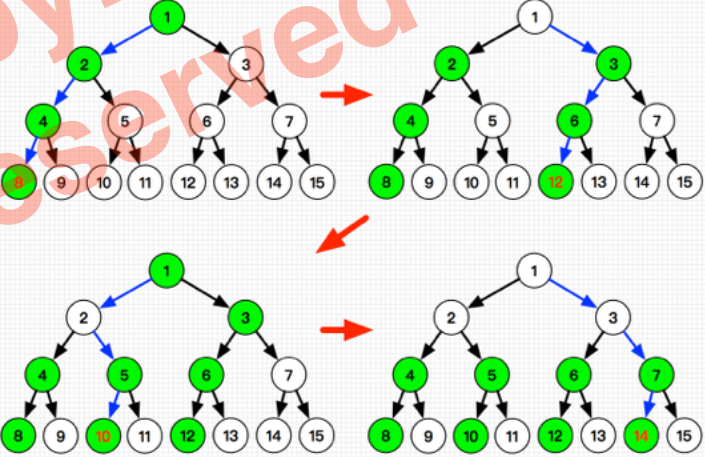
小球下落问题

$2^D-1$个开关排列成深度为D的二叉树，最初都为关闭状态。有n个小球从顶端依次落下，并遵循如下规则：

1. 如果经过一个关闭的开关，则开关打开，小球落向左侧；
2. 如果经过一个打开的开关，则开关关闭，小球落向右侧；

输入D，n，输出最后一个小球最终落到的位置。
样例输入:
4 3
样例输出：
10

//
//  fallingBall.cpp
//  tree
//
//  Created by Ge, Xiao on 01/03/2017.
//  Copyright © 2017 Ge, Xiao. All rights reserved.
//

#include <stdio.h>
#include <iostream>

using namespace std;

class Node{
public:
    Node *left=0,*right=0;  // 左右子树指针
    int id,status=0;   // 开关id,开关状态
    
    Node(int id0){    // 构造函数，可以理解为初始化函数
        id=id0;
    }
    
    int isLeaf() { // 成员方法，返回当前节点是否是叶子
        return left==0 && right==0;
    }

    void addChild(Node *child,int isleft) { // 添加一个新节点/子树
        (isleft ? left : right) = child;    // 直接设置左右子树字段
    }
};

// 构造以id为根节点，深度为d的完全二叉树
Node* buildTree(int id,int depth){
    if (depth==0) { // 递归边界
        return 0;
    }
    Node *node= new Node(id); // 本节点指针
    
    // 递归构造左右子树，深度减一
    node->addChild(buildTree(id*2, depth-1), 1);
    node->addChild(buildTree(id*2+1, depth-1), 0);
    return node;
}

// 模拟一次下落过程
int fall(Node* node){
    node->status ^= 1;   // 改变当前节点开关
    if (node->isLeaf()){ // 到底了，返回当前id
        return node->id;
    }
    return node->status==1 ? fall(node->left) : fall(node->right); // 选择下一层节点
}

int main(int argc, const char * argv[]) {
    int d, n;
    cin>>d>>n;
    Node *root = buildTree(1,d);
    for (int i=0;i<=n-2;i++) { // 模拟前n-1次
        fall(root);
    }
    cout<<fall(root)<<endl;  // 返回最后一次
    return 0;
}

小球下落问题2

与原题一样，改为输出所有叶节点开关状态。
样例输入：
4 3
样例输出：
1 0 1 0 1 0 0 0

完整代码见 fallingball2.cpp

作业题目

1. 证明任何树的节点数N与边数E满足关系E=N-1.
   证明：树中每条边都会连接一个子结点，即树的边数等于树中子结点的个数，又因为根结点不是子结点，故边数E等于树的结点树减1。

2. 用一个四叉树可以表示一个正方形网格的颜色情况，也可以是三角形网格，也可以是梯形网格。
   提示：树的层数表示形状递归的层数。灰色结点表示它的子结点中有黑色和白色两种结点，白色或黑色结点如果有子结点的话，就表示他们的子结点中全是白色或黑色结点。